Forma, Vol. 33 (No. 1), pp. 13-22, 2018
doi:10.5047/forma.2018.003
Original Paper
Coding Rule for Periodic Orbits in the One-dimensional Map
Yoshihiro Yamaguchi
Teikyo Heisei University, Ichihara, Chiba 290-0193, Japan
E-mail address: chaosfractal@iCloud.com
(Received March 20, 2018; Accepted October 17, 2018)
Abstract.
A new coding rule for periodic orbits in unimodal one-dimensional maps is derived. The best-known example of a family of unimodal maps is the logistic map. The band merging is observed in the bifurcation diagram of the logistic map. Let 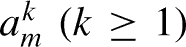 be the critical value at which 2k-band merges into 2k−1-band. At
be the critical value at which 2k-band merges into 2k−1-band. At 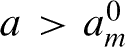 , the diverging orbit appears and thus 1-band disappears. The relations
, the diverging orbit appears and thus 1-band disappears. The relations 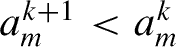 for k ≥ 0 hold. Let sq be the code for periodic orbit of period q in the parameter interval
for k ≥ 0 hold. Let sq be the code for periodic orbit of period q in the parameter interval 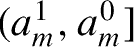 . Assume that the code sq represented by symbols 0 and 1 is known. In the interval
. Assume that the code sq represented by symbols 0 and 1 is known. In the interval 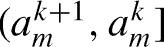 , there exists the periodic orbit of period 2k × q (k ≥ 1). Let its code be s2k × q. Let D be the doubling operator defined by the substitution rules as 0 ⇒ 11 and 1 ⇒ 01. The following coding rule is derived. Operating k times of D to sq, the code s2k × q is determined.
, there exists the periodic orbit of period 2k × q (k ≥ 1). Let its code be s2k × q. Let D be the doubling operator defined by the substitution rules as 0 ⇒ 11 and 1 ⇒ 01. The following coding rule is derived. Operating k times of D to sq, the code s2k × q is determined.
Keywords:
One-dimensional Map, Bifurcation Diagram, Coding Rule, Periodic Orbits, Doubling Operator
[Full text] (PDF 640 KB)
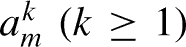 be the critical value at which 2k-band merges into 2k−1-band. At
be the critical value at which 2k-band merges into 2k−1-band. At 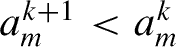 for k ≥ 0 hold. Let sq be the code for periodic orbit of period q in the parameter interval
for k ≥ 0 hold. Let sq be the code for periodic orbit of period q in the parameter interval 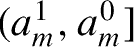 . Assume that the code sq represented by symbols 0 and 1 is known. In the interval
. Assume that the code sq represented by symbols 0 and 1 is known. In the interval 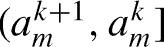 , there exists the periodic orbit of period 2k × q (k ≥ 1). Let its code be s2k × q. Let D be the doubling operator defined by the substitution rules as 0 ⇒ 11 and 1 ⇒ 01. The following coding rule is derived. Operating k times of D to sq, the code s2k × q is determined.
, there exists the periodic orbit of period 2k × q (k ≥ 1). Let its code be s2k × q. Let D be the doubling operator defined by the substitution rules as 0 ⇒ 11 and 1 ⇒ 01. The following coding rule is derived. Operating k times of D to sq, the code s2k × q is determined.